Cartesian Coordinates in Three Dimensions
Points are specified in this system as an order triple, (x, y, z). In two dimensions the equations x = c and y = c represent, respectively, vertical and horizontal lines. In three dimensions they are planes. The figure below depicts the level planes x = 2, y = 2, and z = 3. The horizontal plane is z = 3, the vertical plane on the right is x =2 and the vertical plane forming the back wall is y = 2. The point common to all of these is the point point P with coordinates (2, 2, 3). The figure also depicts how points are located in this system. First we move 2 units along the x–axis to the plan x = 2, this is the point with coordinates (2, 0, 0), and then staying on this plane we move parallel to the y–axis, 2 units to the plane y = 2, arriving at the point (2, 2, 0). Finally, stay on the intersection of the planes x = 2 and y = 2 we move 3 units upward to the point (2, 2, 3).
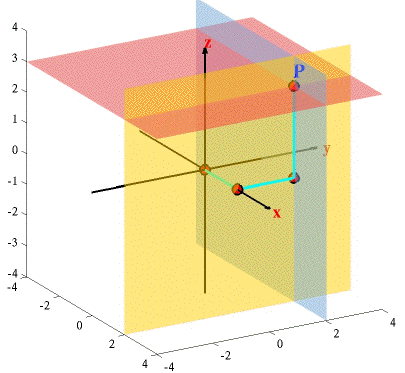The line joining this point to the origin is sometimes denoted as a vector given by v =2i+2j+3k. The length of this line is then the magnitude of v, denoted by
|v| and is computed with the formula
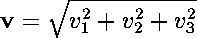
For this vector we have
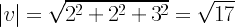
Back