Cylindrical Coordinates in Three Dimensions
Recall polar coordinates in the plane. Points are labeled as (r, q) where r is the distance the point (x, y) is from the origin and q is the angle the line from (0, 0) to (x, y) makes with the positive x–axis. See the figure below.
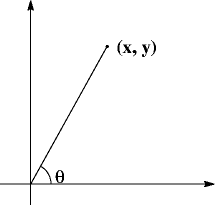
Trigonometry then tells us that
and
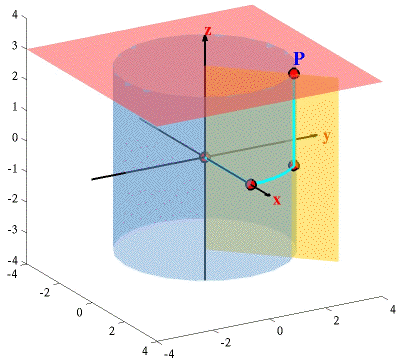
This system projects to three dimensions by simply adding a third coordinate, z. This system is what is known as cylindrical coordinates and a point is denoted by (r, q, z), with r and q defined as above. In polar coordinates the curve r = c, c>0, is a circle of radius c, since we can choose q to be any value. If we add a third coordinate we get points (r, q, z) that are above and below the circle creating the surface known as a circular cylinder. This surface is shown in the figure below. In the plane, the set of points where q = c, is a line through the origin, since we can choose r to be any (positive) value . Adding a third coordinate we we get a plane the contains the z–axis. This is the vertical plane shown in the figure below. The surface z = c is a horizontal plane. The point P on the graph below is given by (
, p/4, 3). Locating this point in this coordinate system is done by moving from the origin along the x–axis units (moves to the circle of radius ), then around the circle of radius 1 by p/4 radians or 45° , finally move this point vertically on the cylinder to the plane z = 3. (This is the point (2, 2, 3).
Back