Many situations require a model that is necessarily a function of several variables. One situation is the wind-chill index shown in the table below.
Given the wind speed, v (in km/h) and the temperature T (in ° C) we read from the table the wind-chill index. For example if the wind speed is 50 km/h (31 mph) and a temperature of -12°C (10.4°F) then the wind-chill index is -37.
This shows that wind-chill index ( WCI) is a function of wind speed ( v) and temperature ( T) and so we write
Functions of two variables have a graphical representation as well. Each pair (v, T) can represent a point in the plane and the wind-chill index associated with this pair represents a height above or below the plane. Connecting the heights with lines produces a surface in three-dimensional space producing a rectangular patched surface, where each corner of the rectangle is a point with coordinates ( v, T, WCI). This graphical representation is shown below.
Another type or graphical representation is a contour graph where the curves where f( v, T) = k (k a constant) are drawn. These are the curves where wind-chill index is the same for a set of wind speeds and temperatures. Below is a contour graph for this function. Each curve is labeled the the wind-chill index it represents. The colorbar to the right shows the color that represents the particular level. Compare this graph with the previous. Can you identify these curves on the surface?
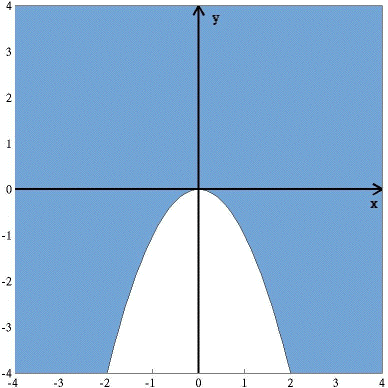
As with functions of one variable, it is important to determine the domain of a function of two or more variables. Consider the function
Since we require that the term under the square root be positive we must have y > –x2. A graph of this domain is shown below and the graph of the surface the function represents follows that.

Some of the first curves that we learn are the line, parabola, circle, ellipse, and hyperbola. These have their counterparts as surfaces in three dimensionsal space. The plane, sphere, paraboloid, ellipsoid, and hyperboloid of one and two sheets. These are as shown below. These of course aren't all representations of functiions. Can you explain why?
| Plane
|
Sphere |
Paraboloid |
|---|---|---|
 |
 |
 |
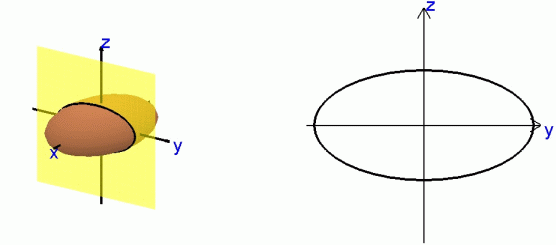
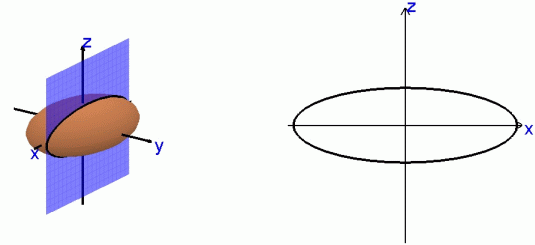
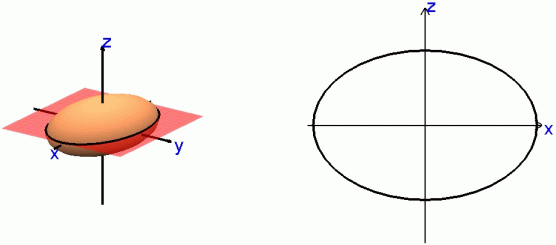
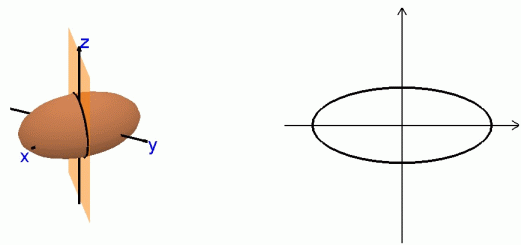
| Ellipsoid
|
Cone
|
Hyperboloid of One Sheet
|
 |
 |
 |
Hyperboloid of Two Sheets
 |
|---|
 |
Another way to understand the structure of a function of two variables is to look at the curves or traces cut by planes that are parallel to the coordinate planes. Consider the surface created by the function f(x,y)= x2 –y2, know as the saddle surface, a hyperbolic paraboloid. This is shown in the figure below.
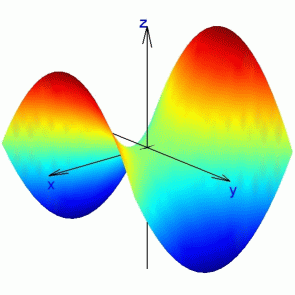
Cutting the surface by the plane x = c, a plane parallel to the xz-plane, produces parabolas that open downward.

Cutting the surface by the plane y = c, a plane parallel to the yz-plane, produces parabolas the open upward.

Cutting the surface by the plane z = c, a plane parallel to the xy-plane, produces hyperbolas. These are also known as the contours or the level curves of the surface. Notice when z = 0, two intersecting lines appear. Why do you suppose this is?

Let's look at this surface a little differently. In particular, when the domain for f(x,y) = x2–y2 is the unit circle instead of the square. When we cut this surface with planes that contain the z-axis, we obtain parabolas that open upward and downward depending on the plane. What is the shape of the surface when the plane cuts the xy-plane in the lines y = x or y = –x?

What follows are the same type of plane cuts, but for the ellipsoid.