Limits

Unlike limits for funtions of one variable, where all is necessary is that we consider the limit from the left and right, limits for functions of two or more variables have an infinite number of ways of approaching a point in the plane. This is demonstrated in the figure below where three different paths to the origin in the plane are shown. These paths are two lines (y = 2x, y = -x/4), a spiral (x = t cos(2pt), y = t sin(2pt)), a parabola (y = x²), and a circle ((x – 1/2)² + (y – 1/2)² = 1/2).

Because of this it is somewhat more difficult to determine if a function has a limit at a given point since it is possible to get different values for a limit depending on the path taken. This is illustrated with the function

If we approach (0, 0) along these paths on the surface we get different values as we near the origin. This is illustrated in the following sequence of graphs. The first is the graph of the function itself. Noticed how the surface is pinched together along the z-axis.

It is for this reason that different limits are obtained along different paths. Below are two graphs which show the paths described above. Note that the path from the line y = x/2 is in red, the parabola y = -x² in blue, and the spiral x = t/2 cos(2 t), y = t/2, sin(2 t) in green.

cuspviews1 (21K)

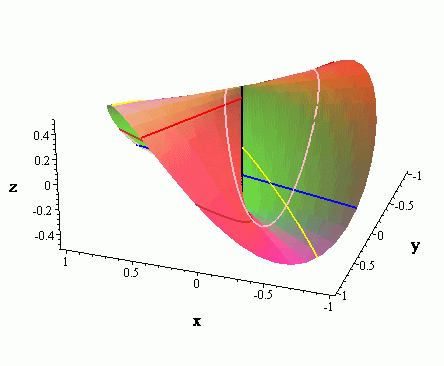
The various limits are calculated algebraically as follows.

For lines,

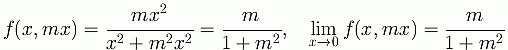
and so the limits are, respectively, 2/5 and -4/17.

For the parabola,

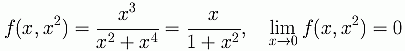
For the spiral,

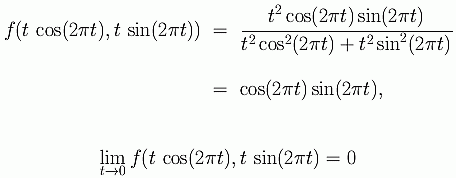
For the circle, (with considerable simplifying),

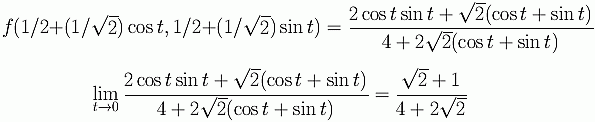
Therefore in order for the limit to exist, it is necessary for the limit to exist along all curves through the limit point and all limit values must be equal. The graph below shows this possiblilty, the same approaching curves from above are used. The function shown is

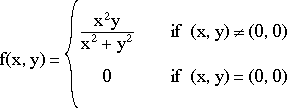
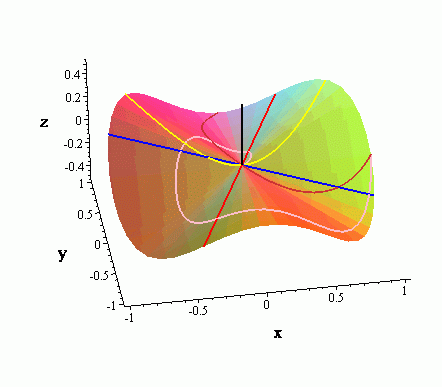
Because of this it is impossible to check all curves. We need another way. One way this is done is to use the inequality

x² ≤ x² + y² and the Squeeze Theorem. This produces the following

and so by the Squeeze Theorem

Back