Spherical Coordinates in Three Dimensions

A point in three dimensional space is designated by spherical coordinates in the following way:

r:		the distance from the origin
q:		the angle rotated from the positive x–axis (azimuth)
f:		the angle rotated from the positive z–axis (declination)

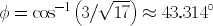The point P in the figures below is the point designated by r = , , and (the cartesian coordinate (2, 2, 3)). The coordinate transformations are the following:

Cone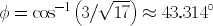

and plane

Cone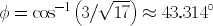

, plane

, and sphere r =

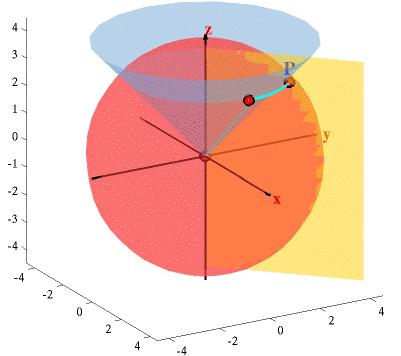The figures above depict the level surfaces for spherical coordinates. The surface r = c, (c > 0) is a sphere of radius c since r is the distance a point is from the origin. So we are looking at all the points that are the same distance from the origin. The surface

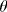= c is a plane containing the z–axis similar to cylindrical coordinates. The surface f = c defines all the points that lie on a line rotated an angle of c radians from the positive z–axis. If we allow r and q to take on any values the surface generated is a cone. The figures above also indicate how a point is located using spherical coordinates. Move from the origin on the cone given by f until a distance r from the origin, all of this is done directly above the x–axis.

Back