Fourier's Approach to Heat Flow
Consider the infinite rectangular lamina, 2 units wide.
![]()
![]()
The equation that models heat flow in this lamina is given by
![]()
Fourier was interested in the equilibrium solution where ![]() and chose the boundary conditions:
and chose the boundary conditions:
![]() and
and ![]() As well as
As well as ![]() bounded as
bounded as ![]() .
.
He assumed that ![]() Substituting this into the equation gives
Substituting this into the equation gives
![]()
Since we can separate this equation into two functions one in x only and one in y only it must be the
case that
![]() a constant.
a constant.
This gives two separate equations:
|
|
|
|
We solve the equation for G first. We have ![]() . Using the boundary conditions
. Using the boundary conditions
we have
![]() and
and ![]()
For arbitrary values of λ this system will have only the trivial solution and we want a nontrivial solution. Adding these
equations gives: ![]() . If
. If ![]() we take
we take ![]() or λ
or λ![]() . Since
. Since ![]()
does not satisfy the boundary conditions we take ![]() We obtain then an infinite number of solutions given by
We obtain then an infinite number of solutions given by
![]()
For the equation ![]() we have
we have 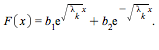 If we require that
If we require that ![]() be
be
bounded then ![]() and so
and so ![]() Therefore we obtain the solutions
Therefore we obtain the solutions
![]()
This then gives the equilibrium solutions as
![]()
Fourier then noted that, the principle of superposition, that the general solution has the form
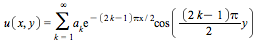
and from the boundary condition ![]() we have to choose the values
we have to choose the values ![]() to satisfy
to satisfy
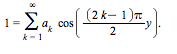 (A)
(A)
Fourier differentiated this expression and infinite number of times and generated a system for the infinite number of unknowns
![]() . He offered no justification why term-by-term differentiation was possible. Later on he noted the orthogonality of the functions
. He offered no justification why term-by-term differentiation was possible. Later on he noted the orthogonality of the functions
![]() on the interval [-1, 1]. i.e.
on the interval [-1, 1]. i.e.
![]()
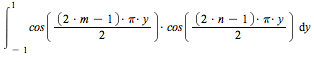
![]()
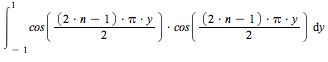
![]()
Fourier then multiplies (A) by ![]() and integrates term-by-term, again with no justification.
and integrates term-by-term, again with no justification.
Note that the only nonzero term is when ![]() and we arrive at
and we arrive at
![]()
![a[k] := int(cos(1/2*(2*k-1)*Pi*y), y = -1 .. 1)](images/FouierHeatEq_49.gif)
![]()
![]()
![]()
The solution is then given by the infinite series
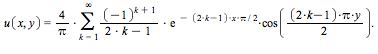
Let's consider partial sums of this function.
*exp(-1/2*(2*k-1)*x*Pi)*cos(1/2*(2*k-1)*Pi*y), k = 1 .. n) end proc](images/FouierHeatEq_54.gif)
*exp(-1/2*(2*k-1)*x*Pi)*cos(1/2*(2*k-1)*Pi*y), k = 1 .. n) end proc](images/FouierHeatEq_55.gif)
Graphs of this function for ![]() and various values of
and various values of ![]() are shown below.
are shown below.
![]()
![]()
![]()
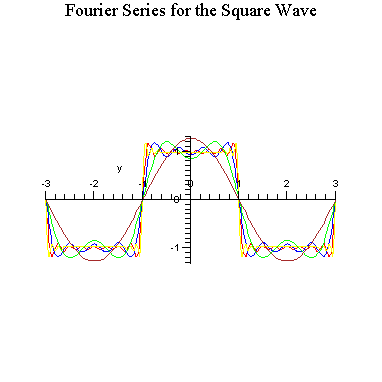
How do these partial sums converge to the square wave.
![]()
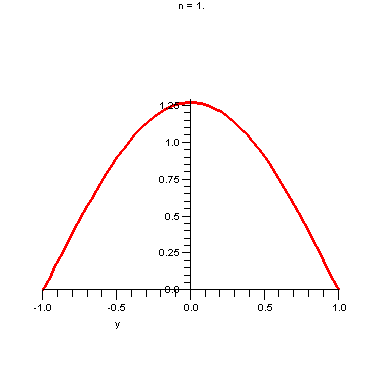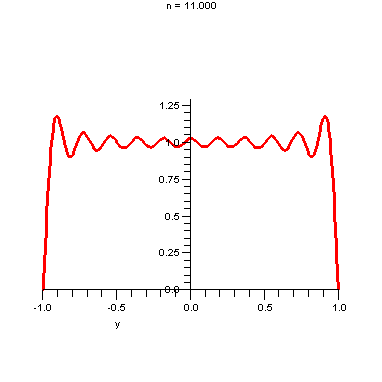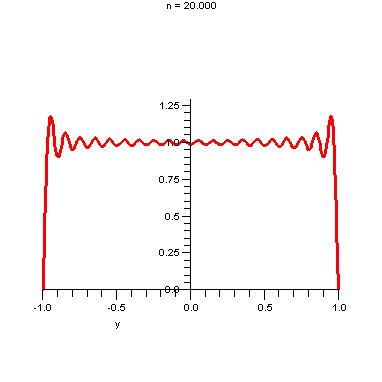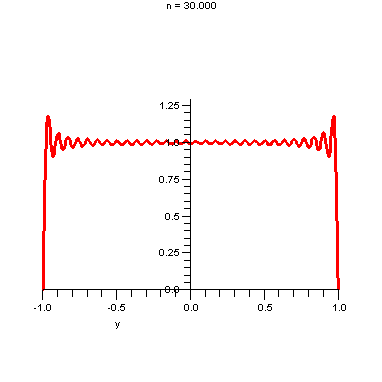
Notice that it overshoots near the enpoints of the interval. This is known and the Gibbs-Wilbraham phenomenom.
For a three dimensional veiw of the solution we plot the temperature variation on the rectangle [0, 2]×[-1,1].
![]()
![]()

Also
![]()
![]()
